|
-
- 1.
- In a certain game, there are three piles of stones: one with 22 stones,
one with 14 stones, and one with 12 stones. At each turn, you can double the
number of stones in a pile by transferring stones to it from one other pile.
(For example, your first move can be to transfer 12 stones from the first pile
to the third pile.) The game ends if the three piles are equal in size. Can
you find a way to end the game in three moves?
- 2.
- Imagine a corridor with 2002 light switches. Initially, all the lights are
off. Then 2002 people walk through the corridor, one after the other. The
first person flips every switch, the second person flips every other switch
(starting with the second), the third person flips every third switch
(starting with the third), and so on. After all the people have gone through,
which lights are on and which are off?
- 3.
- Show that you cannot cover a circular disk with two circular disks of
smaller diameter.
- 4.
- Three bugs are crawling on the coordinate plane. They move one at a time,
and each bug will only crawl in a direction parallel to the line joining the
other two.
- (a)
- If the bugs start out at (0,0), (3,0), and (0,3), is it possible that
after some time the first bug will end up back where it started, while the
other two bugs switch places?
- (b)
- Can the three bugs end up at (1,2), (2,5), and (-2,3)?
- 5.
- Suppose 15 pennies are arranged in a triangle, as in the following
diagram:
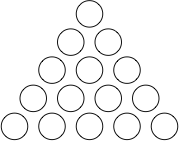
Show that inside this triangle, there is guaranteed to be an equilaterial
triangle in which all the vertex pennies are facing the same way (either all
heads up or all tails up).
- 6.
- The decimal expansion of the fraction 1/11 = .090909... consists of the
two digits 09 repeating over and over; we say that this decimal expansion has
period length 2. Similarly, the decimal expansion of 1/37 =
.027027027... has period length 3. Can you find other integers n such
that the decimal expansion of 1/n has period length 2? period length 3?
Can you find all the prime numbers p such that the decimal expansion of
1/p has period length 6 or less? Can you find any prime numbers
p so that the octal (i.e., base 8) expansion of 1/p has period
length 3?
- 7.
- You are a secret agent assigned to carry out classified research on Enemy
Government Gadgets (EGGs). Your mission: to determine the highest floor of an
office building from which a dropped EGG will survive falling to the ground.
Your method: drop an EGG from different floors and see if it breaks.
- (a)
- The budget is tight at the agency, so you'll only have one EGG to work
with. Once that EGG breaks, that's it. How can you determine the highest
floor that is safe for EGG dropping? Are there any other strategies?
- (b)
- Your department has realized the importance of your mission, and has
stretched the budget to allow for 2 EGGs. However, time is of the essence so
you must guarantee that you can finish your mission within 10 drops. What is
the tallest building for which you can be assured of getting a precise
answer, even with the worst possible luck?
- (c)
- Generalize the problem: if the agency gives you 2 EGGs, and you
are allowed k trials, what is the tallest building that you can
analyze? What if you are allowed k trials with 3 EGGs? What about
k trials with n EGGs?
- 8.
- (Proposed by Taktin Oey, student, Mathcamp 2001.) A computer is programmed
in the following way. First it prints a random digit between 0 and 9 (with
equal likelihood for each possible digit). Then it picks between the commands
"break" and "continue", again randomly with equal probability. If it picks
"continue", the process repeats; if it picks "break", the program terminates.
What is the probability that the final output is a palindrome? (For example,
if the program runs as "0, continue, 1, continue, 3, continue, 3, continue, 1,
continue, 0, break", then the output is 013310. It reads the same forward and
backward, and is thus a palindrome.)
- 9.
- The Seven Dwarfs are having breakfast, and Snow White has just poured them
some milk. Before drinking, the dwarfs have a ritual. First, Dwarf #1 splits
his milk equally among his brothers' mugs (leaving himself with nothing). Then
Dwarf #2 does the same with his milk, etc. The process continues around the
table, until Dwarf #7 has distributed his milk in this way. At the end, each
dwarf has exactly the same amount of milk as he started with! If the total
amount of milk was 42 ounces, how much milk did each dwarf have at the
beginning? Is this the only possible distribution of milk, or does the problem
admit multiple solutions? (Be sure to justify your answer.)
- 10.
- A single peg is placed at the bottom left-hand corner of a grid that
extends infinitely far up and to the right. You play a game in which you are
allowed to make the following move: if the hole immediately above and the hole
immediately to the right of a peg are both empty, you can remove the existing
peg and place pegs in those two holes instead. Below are some sample moves.
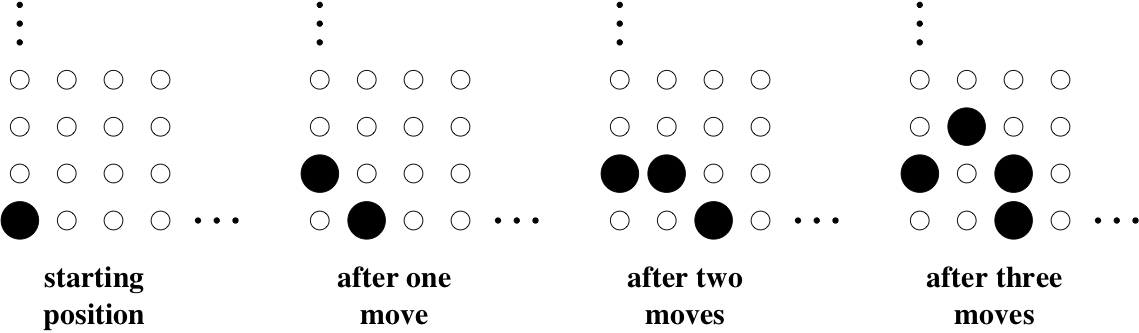
- (a)
- Show that, no matter how you move, you can never remove all the pegs
from the 3-by-3 square at the bottom left-hand corner of the grid.
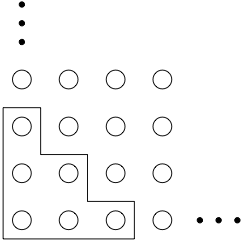
- (b)
- Is it possible to remove all the pegs from the six holes closest to the
bottom left-hand corner of the grid (the region indicated in the picture
below)?
|