2020 Qualifying Quiz

1. Caitlin wants to draw n straight line segments, without lifting her pencil off the paper and without retracing her path, so that each segment crosses exactly one other segment (not counting intersections at vertices) and she ends up back where she started.
   1. Show how she can do this for n = 6. (Draw a picture!)
   2. For which n can it be done, and for which n is it impossible? Prove your answer.
2. Here is a table of remainders when powers of 10 are divided by 2020:

   k	10k	Remainder
   0	1	1
   1	10	10
   2	100	100
   3	1000	1000
   4	10000	1920
   5	100000	1020
   6	1000000	100
   7	10000000	1000
   8	100000000	1920
   9	1000000000	1020

   We see that the remainders repeat every four steps (period 4), with two exceptions at the beginning, 1 and 10. We will call a sequence that repeats with period 4, with two exceptions at the beginning, a fortuitous sequence (four-two-itous). Sequences that have periods smaller than four (e.g. sequences that repeat every two steps) do not count as fortuitous.
   1. In addition to 2020, for what other values of m is the sequence of remainders when 10^k is divided by m a fortuitous sequence?
   2. In addition to 10, for what other values of a is the sequence of remainders when a^k is divided by 2020 a fortuitous sequence?
   You might find it helpful to look up the Chinese Remainder Theorem (for instance, at www.cut-the-knot.org/blue/chinese.shtml).
3. An island has two cities: Mathopolis and Campville. There are three roads connecting the cities: Red Road, Green Road, and Blue Road. The roads can intersect each other, but only at right angles. Also, no road intersects itself. (Unlike in the example below, roads don't always go left to right – they can loop around and cross however they want, obeying the restrictions.) All along each road, there are signposts indicating the direction to Campville.
   
   There are six types of intersections, which we divide into two groups: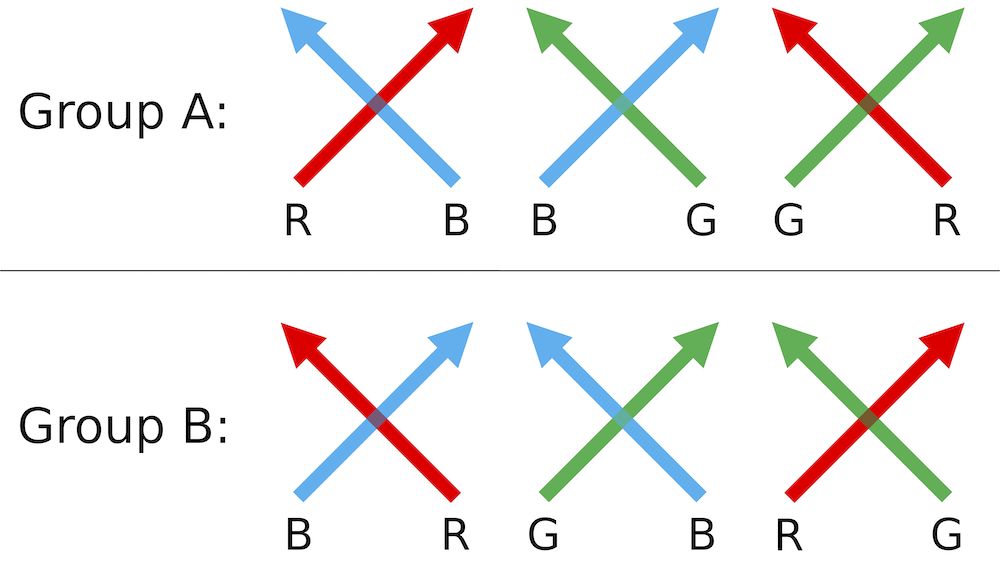 Note that each group has a red-green intersection, a red-blue intersections, and a blue-green intersection. The intersections in the two groups are mirror images of each other.
   
   In the example below, the red-blue crossing belongs to group A, and the red-green and green-blue crossings belong to group B.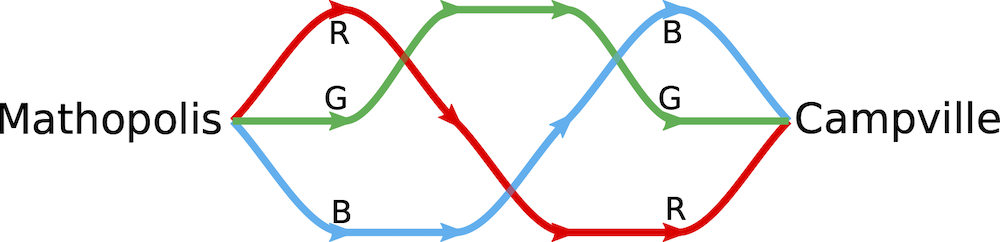 Let a be the number of intersections in Group A, and b the number in Group B.
   1. Find, with proof, the set of possible values of a - b under the assumption that Red Road does not intersect Green Road.
   2. Find the set of possible values of a - b, without the extra assumption.
   Note: This is one of those problems where you might quickly get the right idea but then struggle to write it down. Keep trying! If all you have is a vague, wordy, handwavy explanation, then you're not done with the problem: you haven't found the right way of thinking about it yet, haven't discovered its true essence. Once you do, the long, wordy explanation will suddenly transform into a clear, step-by-step, logical argument. (That said, any explanation is better than none; do the best you can, and send us what you have.)
4. Mathematical Chunks of Sentient Protoplasm (MCSPs, for short) are smart blobs who dream of merging together into one huge blob. But they can only do it following certain rules:
   • If two MCSPs have the same mass, or if their masses are 1 apart, they can merge into a single MCSP, whose mass will be the sum of the original two.
   • If an MCSP has even mass, it can split into two MCSPs, each with half the original mass.
   Suppose we start with n MCSPs, with masses 1 through n. For what values of n is there a finite sequence of steps that will allow all n MCSPs to merge together into a single MCSP and achieve their dream of unity?
5. Given a sequence of numbers, its head length is the largest integer m for which the first m terms are nondecreasing. For instance, the head length of [1, 1, 2, 4, 3] is 4. Thus, we can compute the average head length for any set of sequences. For example, we can evaluate the head lengths for all six permutations of the sequence [1, 2, 3]:
   • [2, 1, 3], [3, 1, 2], and [3, 2, 1] each have head length 1,
   • [1, 3, 2] and [2, 3, 1] have head length 2, and
   • [1, 2, 3] has head length 3.
   Thus, a permutation of [1, 2, 3] has average head length (1 + 1 + 1 + 2 + 2 + 3)/6 = 5/3.
   
   Let n be a positive integer.
   1. Consider all the permutations of [1, 2, …, n].
      1. What fraction of them has head length 1?
      2. What fraction of them has head length k, for k < n?
      3. What is the average head length of a permutation of [1, 2, …, n]?
   2. What is the average head length of a permutation of [1, 1, 2, 3, …, n]?
   3. What is the average head length of a sequence of length n consisting of the numbers {1, 2, 3, 4}?

   In each case, please express your answer as an explicit (rather than recursive) formula in terms of n. You may use sigma notation in your answers.

6. Harini loves solving quadratic equations, but only if they have real roots. She starts with an equation
   x² + p₁x + q₁ = 0
   with p₁, q₁ not both 0. If the equation has two real roots, Harini uses them to create a new quadratic equation,
   x² + p₂x + q₂ = 0,
   using the smaller of the two roots as p₂ and the larger one as q₂. For instance, if Harini's first equation was x² + 2x − 3 = 0, which has roots −3 and 1, then her second equation would be x² − 3x + 1 = 0. She keeps going in this way: at each step n, if the equation
   x² + p_nx + q_n = 0
   has two real roots, Harini uses them as the coefficients of the next equation,
   x² + p_n+1x + q_n+1 = 0,
   always with the smaller root as p_n+1 and the larger root as q_n+1. (A repeated root counts as two equal roots, in which case p_n+1 = q_n+1.) She stops when she gets to an equation that does not have real roots.
   1. Prove that this process cannot continue forever.
   2. What is the maximal possible length of Harini's sequence of equations?

Problem #4 is due to Alvin Chen, MC '18–'19. Problem #5 is due to Sean Li, MC '18. All other problems were written by the Mathcamp staff.