2019 Qualifying Quiz
-
If you take a scientific calculator, type in any number, and then alternate applying the operations ATAN and COS, then eventually you will reach a point where you run into a cycle: after every COS step, you will see a result of approximately 0.786 (and after every ATAN step, a result of approximately 0.666 radians, or 38.2 degrees).
- Find a formula for the number you get by starting with 0 and then applying the procedure "apply ATAN and then COS" n times. (You may give either an explicit formula or a recursive formula. In either case, you should try to make the formula as simple as possible.)
- Find an exact formula for the 0.786 number. (You do not need to prove that the formula that you found in part (a) converges to this number.)
-
Susan and Eric are playing a dice game, with standard six-sided dice which have an equal probability of rolling each integer from 1 through 6. Each player takes turns scoring points as follows.
On Susan's turn, she rolls a die. If it's a 1, she rolls two dice in its place, continuing to replace any 1s by two new dice. When finally no 1s are showing, Susan scores points equal to the sum of the remaining dice, and then her turn ends. (For example, suppose she rolls a 1. Then it gets replaced by two dice; if these are a 3 and a 1, the 3 remains and the 1 gets replaced by two more; if these are a 2 and a 4, then Susan stops and scores 3 + 2 + 4 = 9 points.)
On Eric's turn, he rolls a die. If it's even, he replaces it with a roll of two dice; if the new total is even, he replaces it with a roll of three dice, etc. He continues to roll one more die than previously as long as his total is even. When he finally rolls an odd total, Eric scores that many points, and then his turn ends.
On average, how many points do Susan and Eric each score on a turn?
-
In the game of Flip Flop, players stand in a circle and take turns saying the numbers 1, 2, 3, etc., going clockwise.
When they get to a multiple of 7, the player whose turn it is says FLIP instead, and the direction switches: if they were going clockwise before, they now go counterclockwise, or vice versa.
When they get to a multiple if 8, the player whose turn it is says FLOP instead. The direction stays the same, but the next person is skipped over.
For a number n that is a multiple of both 7 and 8, the player says FLIP FLOP. Direction reverses and you skip over the next person. This means n + 1 is said by the person who said n - 2.
- Show that no matter how many people are in the circle, eventually each person will get a turn to speak.
- Suppose we replace 7 and 8 by arbitrary integers K and M respectively. For what values of K, M is every player eventually guaranteed get a turn to speak (regardless of the number of players)?
-
There is a puzzle with N2 pieces, each one shaped like a wedge that is 1/N of a disk. On the front of each piece, each of the two sides of the wedge is labeled with an integer between 1 and N, so that each of the N2 possible ordered pairs occurs exactly once. The goal of the puzzle is to form N full disks in such a way that the edges come together to have the same label. Below is an example of some pieces fitting together to form a full disk when N = 5.
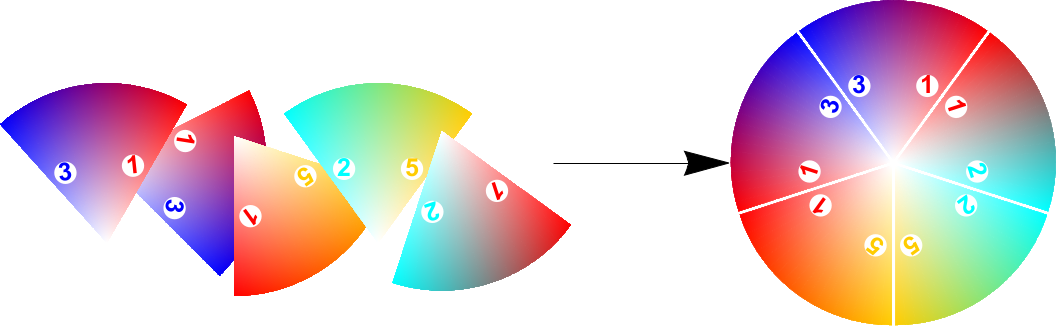
- Show that the puzzle can be solved when N = 5.
- Show that the puzzle can be solved for any integer N ≥ 3. Partial credit will be awarded for a proof that the puzzle can be solved for infinitely many N.
-
Every day at noon exactly, people submit orders of positive integer numbers of paninis at your panini store. It takes you 1 minute to make 1 panini.
When Alice orders 2 paninis and Bob orders 100 paninis, you decide to make Alice's paninis first, because it results in less total customer wait time (104 vs. 202 minutes).
- [Warm-up exercise: do not submit an answer] Show that for any set of orders, you achieve the smallest total wait time by processing the smaller orders first.
When the town gets wind of your scheme, they hatch devious plans. Instead of ordering 100 paninis, Bob decides to submit 100 orders of 1 panini each under different names, so he gets processed first. Oh no.
Call a panini-making scheme strategy-free if no customer, in any scenario, can strictly decrease their average wait time just by splitting their order up into several smaller (integer-size) orders.
Assume your customers are aware of your scheme and will not split up their orders if the scheme is strategy-free.
- Show that the scheme "choose the sequence of orders uniformly at random" is strategy-free.
- Give an example of a strategy-free scheme that has a lower average wait time than the above scheme whenever the orders are not all the same size.
- Suppose you know that, on any given day, you will either receive (1) three orders for one panini each, or (2) one order for one panini and one order for two paninis. Give a strategy-free panini-making scheme such that in either scenario (1) or (2), the average total wait time is at most 25/24 the optimal total wait time.
-
Jennifer and Serena are playing a game called Candy Split. They start with two piles of candy, one of size M and one of size K. On a player's turn, she eats one of the piles and splits the other pile into two (non-empty) piles any way she wants. Whoever can't make a legal move (i.e. is presented with two piles of one candy each) loses. Note that eating as much candy as possible is not the object of the game, though it may be a pleasant side effect.
- [Warm-up exercise: do not submit an answer] Serena gets to decide whether to go first or second. What should she do when M = 2018 and K = 2019? What about for general values of M and K? (Hint: it's all about the parity of M and K.)
The reason we're not asking you to submit an answer for the warm-up exercise is that it's a famous problem that can be found in many places on the internet. (Feel free to look it up if you can't figure out the answer.) What we are really interested is a harder problem:
Suppose Jennifer and Serena have three different types of candy. The game is now played with six piles of candy, two piles of each type. On a player's turn, she chooses a type of candy, eats one of the piles of that type, and splits the other. Whoever can't move loses. If the numbers are (M1, K1), (M2, K2) and (M3, K3), is it better to go first or second, and what is the winning strategy?
In order to solve this problem, you will need to learn a little bit of combinatorial game theory at this link: www.mathcamp.org/2019/cgt.pdf.
-
Fill out the following table of nimvalues for Candy Split. The (M,K) entry of your table should show the nimvalue of the game with piles of size M and K.
M\K 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
- The game is (2,4), (1,8), and (3,5). It is Serena's turn. What should she do? Explain how to derive the answer from your table.
-
Can you see a pattern in the table? If not, try enlarging the table some more until you see it. (Feel free to use a computer if you'd like, but you can certainly solve the problem without it.)
Based on your conjectured pattern, write down a formula (or algorithm) for computing the nimvalue of (M,K) for all M and K. If you can, prove your formula! - The game is (2,4), (1,8), and (2019, 2030). It is Serena's turn. What should she do? Explain how to derive the answer from your formula or pattern (even if you haven't proved it).
All problems were written by the Mathcamp staff.





