Mathcamp 2000 Quiz

2000 Qualifying Quiz

You may also be interested in the printable (PDF) format or the LaTeX source code.

Problems

1.

Imagine a corridor with 100 light switches. 100 people walk through the corridor one after another. The first person flips every switch, the second person flips every other switch (starting with the second), the third person flips every third switch (starting with the third), etc. At the end, which switches are on and which are off?

2.

Find the smallest positive integer n such that

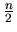is the square of an integer,

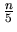is the fifth power of an integer,

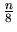is the eighth power of an integer, and

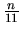is the eleventh power of an integer.

3.

A triangle has sides of length a, b and c, and they satisfy the equation 1/(a+b) + 1/(a+c) = 3/(a+b+c). Determine the angle opposite the side of length a.

4.

Yuliya rolls a pair of fair dice four times. What is the probability that she rolls at least a 10, at least two times?

5.

Do there exist 1,000,000 consecutive composite numbers? If not, why not? If so, do you have any ideas on how to find them?

6.

Find all integers x, y, and n such that xy²(x+y²)= 2ⁿ.

7.

Three bugs are crawling on the coordinate plane. They move one at a time, and each bug crawls in a direction parallel to the line joining the other two.

(a): If the bugs start out at (0,0), (3,0), and (0,3), is it possible that after some time the first bug will end up back where it started, while the other two switch places?
(b): Can the three bugs end up at (1,2), (2,5), and (-2,3)?

8.

You are a secret agent assigned to carry out classified research on the C_n-tower, an ultra-modern office block n stories tall. Your mission: to determine the highest floor of the building from which a dropped egg will survive falling to the ground. Your equipment: a supply of exactly k eggs.

(a): Suppose k=1: you have only one egg (and once it smashes, that's it). How can you determine the highest floor that is safe? Are there any other strategies?
(b): Suppose k=2. You need to complete your mission as quickly as possible. What strategy should you use to determine the safe height efficiently? (Here ``efficiently'' means that the worst case scenario takes as few test drops as possible.)
(c): Can you find an answer for higher values of k?

9.

Let a₀ = 1 and 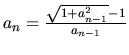$a_n = (sqrt(1+a_{n-1}^2) - 1) / a_(n-1)$ . Show that

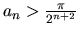10.

Let S₁, S₂, and S₃ be three spheres in three-dimensional space whose centres are not collinear. Let

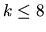be the number of planes which are tangent to all three spheres. Let A_i, B_i, and C_i be the point of tangency between the i^th such tangent plane (

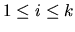) and S₁, S₂, and S₃ respectively, and let O_i be the circumcentre of triangle A_i B_i C_i. Prove that the O_i are all collinear. (If k=0, this statement is vacuously true.)

Optional Project

P.

What is the probability that a random chord on a circle is longer than the side of an inscribed equilateral triangle?

(a): Can you give mathematical arguments for 3 (or even more) different answers!? Is there a correct solution? What do you think might be the source of the paradox?
(b): Suppose we try to resolve the paradox experimentally: draw a circle on the floor, drop 100 straws on it, and calculate what percentage of them cuts a chord that is longer than the side of an inscribed equilateral triangle. (Some straws might miss the circle entirely; let's ignore those, since they don't cut any chord at all.) Which of the numbers from part (a) do you think you will get, and why? (If you wish, you can try doing the experiment and reporting on your results!)